Асимптоты графика функций: их виды, примеры решений. Прямая линия

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

В = С = 0, А ≠0 – прямая совпадает с осью Оу

А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Уравнение прямой по точке и вектору нормали

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0.

Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно (3, -1).

Решение . Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно, С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M 2 (x 2 , y 2 , z 2), тогда уравнение прямой, проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х 2 и х = х 1 , если х 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой.

Пример . Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту

Если общее Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом k .

Уравнение прямой по точке и направляющему вектору

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор (α 1 , α 2), компоненты которого удовлетворяют условию А α 1 + В α 2 = 0 называется направляющим вектором прямой

Ах + Ву + С = 0.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

Уравнение прямой в отрезках

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой

Если обе части уравнения Ах + Ву + С = 0 умножить на число , которое называется нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 –

нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример . Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

уравнение этой прямой в отрезках:

уравнение этой прямой с угловым коэффициентом: (делим на 5)

; cos φ = 12/13; sin φ= -5/13; p = 5.

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

Пример . Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см 2 .

Решение. Уравнение прямой имеет вид: , ab /2 = 8; ab=16; a=4, a=-4. a = -4 < 0 не подходит по условию задачи. Итого: или х + у – 4 = 0.

Пример . Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Решение . Уравнение прямой имеет вид: , где х 1 = у 1 = 0; x 2 = -2; y 2 = -3.

Угол между прямыми на плоскости

Определение. Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми будет определяться как

.

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны, если k 1 = -1/ k 2 .

Теорема. Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты А 1 = λА, В 1 = λВ. Если еще и С 1 = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b представляется уравнением:

Расстояние от точки до прямой

Теорема. Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С =0 определяется как

.

Доказательство. Пусть точка М 1 (х 1 , у 1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М 1:

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x – x 0) + B(y – y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Пример . Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k 1 = -3; k 2 = 2; tgφ = ; φ= π /4.

Пример . Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Решение . Находим: k 1 = 3/5, k 2 = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример . Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение . Находим уравнение стороны АВ: ; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b . k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3 x + 2 y – 34 = 0.

Уравнение

Ах+Ву+С=0

(где А, В, С могут иметь любые значения, лишь бы коэффициенты А, В не были нулями оба сразу) представляет прямую линию . Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой .

Если А х параллельную оси ОХ .

Если В =0, то есть уравнение не содержит у , то оно представляет прямую, параллельную оси ОY .

Когла В не равно нулю, то общее уравнение прямой можно разрешить относительно ординаты у , тогда оно преобразуется к виду

(где a=-A/B ; b=-C/B ).

Аналогично, при А отличным от нуля общее уравнение прямой можно разрешить относительно х .

Если С =0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат

5.

Уравнение прямой, проходящей через данную точку A (x 1 , y 1) в данном направлении, определяемом угловым коэффициентом k ,

y - y 1 = k (x - x 1). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x 1 , y 1), которая называется центром пучка.

. Уравнение прямой, проходящей через две точки: A (x 1 , y 1) и B (x 2 , y 2), записывается так:

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

7Уравнение прямой в отрезках

Если в общем уравнении прямой , то разделив (1) на , получаем уравнение прямой в отрезках

где , . Прямая пересекает ось в точке , ось в точке .

8Формула: Угол между прямыми на плоскости

Уголα между двумя прямыми, заданными уравнениями: y=k 1 x+b 1 (первая прямая) и y=k 2 x+b 2 (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1 й прямой ко 2 й против часовой стрелки ):

9 Взаимное расположение двух прямых на плоскости .

Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1) если , то прямые и совпадают;

2) если , то прямые и

параллельные;

3) если , то прямые пересекаются.

Доказательство. Условие равносильно коллинеарности нормальных векторов данных прямых:

Поэтому, если , то и прямые пересекаются.

Если же , то , , иуравнение прямой принимает вид:

Или , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.

Теорема доказана.

Для определения расстояния от точки до прямой необходимо знать уравнения прямой и координаты точки в декартовой системе координат. Расстоянием от точки до прямой будет являться перпендикуляр, проведенный из этой точки к прямой.

Инструкция

Общее уравнение прямой в декартовых координатах имеет вид Ax+By+C=0, где A, B и C - известные числа. Пусть точка O имеет координаты (x1, y1) в декартовой системе координат.

В этом случае отклонение этой точки от прямой равно δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)), если C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

Расстояние от точки до прямой - это модуль отклонения точки от прямой, то есть r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))|, если C<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

Пусть теперь точка с координатами (x1, y1, z1) задана в трехмерном пространстве. Прямая может быть задана параметрически, системой из трех уравнений: x = x0+ta, y = y0+tb, z = z0+tc, где t - действительное число. Расстояние от точки до прямой можно найти как минимальное от этой точки до произвольной точки прямой. Коэффициент t этой точки равен tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2))

Расстояние от точки (x1, y1) до прямой можно посчитать и в случае, если прямая задана уравнением с угловым коэффициентом: y = kx+b. Тогда уравнение перпендикулярной ей прямой будет иметь вид: y = (-1/k)x+a. Далее нужно учесть, что эта прямая должна проходить через точку (x1, y1). Отсюда находится число a. После преобразований находится и расстояние между точкой и прямой.

31 . Базис на плоскости и в пространстве

Определение. Базисом на плоскости называются два любых линейно независимых вектора.

два любых неколлинеарных вектора образуют базис. Пусть a любой вектор на плоскости, а векторы b и c образуют базис. Так как на плоскости всякие три вектора линейно зависимы, то вектор a линейно выражается через векторы базиса, т. е. выполняется соотношение

Определение. Базисом в пространстве называются три любых линейно независимых вектора. три любых некомпланарных вектора образуют базис. Как и в случае плоскости, устанавливается, что любой вектор a разлагается по векторам b , c и d

Общее определение (чтобы понятно всем было) Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы образуют базис в декартовом координатном пространстве Oxyz.

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

• прямые пересекаются;

• прямые параллельны;

• прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение . Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

. C = 0, А ≠0, В ≠ 0 - прямая проходит через начало координат

. А = 0, В ≠0, С ≠0 { By + C = 0} - прямая параллельна оси Ох

. В = 0, А ≠0, С ≠ 0 { Ax + C = 0} - прямая параллельна оси Оу

. В = С = 0, А ≠0 - прямая совпадает с осью Оу

. А = С = 0, В ≠0 - прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких - либо заданных

начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение . В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой, заданной уравнением

Ах + Ву + С = 0.

Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение . Составим при А = 3 и В = -1 уравнение прямой: 3х - у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 - 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х - у - 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой ,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х 2 и х = х 1 , если х 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой .

Пример . Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение . Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение . Каждый ненулевой вектор (α 1 , α 2) , компоненты которого удовлетворяют условию

Аα 1 + Вα 2 = 0 называется направляющим вектором прямой.

Ах + Ву + С = 0.

Пример . Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение . Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3 , т.е. искомое уравнение:

х + у - 3 = 0

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на -С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b - координатой точки пересечения прямой с осью Оу.

Пример . Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 - нормальное уравнение прямой .

Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0.

р - длина перпендикуляра, опущенного из начала координат на прямую,

а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример . Дано общее уравнение прямой 12х - 5у - 65 = 0 . Требуется написать различные типы уравнений

этой прямой.

Уравнение этой прямой в отрезках :

Уравнение этой прямой с угловым коэффициентом : (делим на 5)

Уравнение прямой :

cos φ = 12/13; sin φ= -5/13; p = 5.

Следует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые,

параллельные осям или проходящие через начало координат.

Угол между прямыми на плоскости.

Определение . Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми

будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны,

если k 1 = -1/ k 2 .

Теорема .

Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты

А 1 = λА, В 1 = λВ . Если еще и С 1 = λС , то прямые совпадают. Координаты точки пересечения двух прямых

находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.

Определение . Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b

представляется уравнением:

Расстояние от точки до прямой.

Теорема . Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С = 0 определяется как:

Доказательство . Пусть точка М 1 (х 1 , у 1) - основание перпендикуляра, опущенного из точки М на заданную

прямую. Тогда расстояние между точками М и М 1 :

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы - это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно

заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.

Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.

Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.

Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты

Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.

Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:

При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .

Замечание:

Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:

(рис. сверху).

самостоятельно, а затем посмотреть решения

Пример 2. Найти асимптоты графика функции .

Пример 3. Найти асимптоты графика функции

Горизонтальные асимптоты

Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ), то y = b – горизонтальная асимптота кривой y = f (x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

Пример 5. График функции

при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении "икса" к минус бесконечности равен нулю:

Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении "икса" к плюс бесконечности равен бесконечности:

Наклонные асимптоты

Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число - точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше - угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё - уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.

Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:

(1)

(2)

Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.

В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.

При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.

При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример 6. Найти асимптоты графика функции

Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.

Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:

Следовательно, x = 0 – вертикальная асимптота графика данной функции.

Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:

Выясним наличие наклонной асимптоты:

Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).

Пример 7. Найти асимптоты графика функции

Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:

Заключение: x = −1 - точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.

Ищем наклонные асимптоты. Так как данная функция - дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой - наклонной асимптоты:

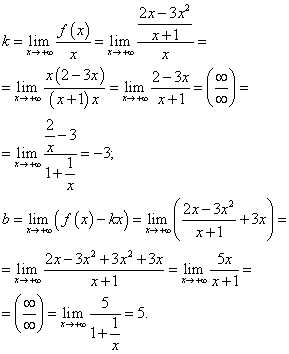
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:

y = −3x + 5 .

На рисунке график функции обозначен бордовым цветом, а асимптоты - чёрным.

Пример 8. Найти асимптоты графика функции

Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:

.

Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .

Пример 9. Найти асимптоты графика функции

Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .

Рассмотрим правосторонний предел при (левосторонний предел не существует):

.

Точка x = 2 - точка разрыва второго рода, поэтому прямая x = 2 - вертикальная асимптота графика данной функции.

Ищем наклонные асимптоты:

Итак, y = x + 1 - наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :

Итак, y = −x − 1 - наклонная асимптота при .

Пример 10. Найти асимптоты графика функции

Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .