Уравнение касательной к графику функции. Дифференциальные уравнения, не разрешенные относительно производной

Пусть дана функция f , которая в некоторой точке x 0 имеет конечную производную f (x 0). Тогда прямая, проходящая через точку (x 0 ; f (x 0)), имеющая угловой коэффициент f ’(x 0), называется касательной.

А что будет, если производная в точке x 0 не существует? Возможны два варианта:

1. Касательная к графику тоже не существует. Классический пример - функция y = |x | в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π /2).

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b , где k - угловой коэффициент. Касательная - не исключение, и чтобы составить ее уравнение в некоторой точке x 0 , достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f (x ), которая имеет производную y = f ’(x ) на отрезке . Тогда в любой точке x 0 ∈ (a ; b ) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x 0) · (x − x 0) + f (x 0)

Здесь f ’(x 0) - значение производной в точке x 0 , а f (x 0) - значение самой функции.

Задача. Дана функция y = x 3 . Составить уравнение касательной к графику этой функции в точке x 0 = 2.

Уравнение касательной: y = f ’(x 0) · (x − x 0) + f (x 0). Точка x 0 = 2 нам дана, а вот значения f (x 0) и f ’(x 0) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x 0) = f (2) = 2 3 = 8;
Теперь найдем производную: f ’(x ) = (x 3)’ = 3x 2 ;
Подставляем в производную x 0 = 2: f ’(x 0) = f ’(2) = 3 · 2 2 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.

Задача. Составить уравнение касательной к графику функции f (x ) = 2sin x + 5 в точке x 0 = π /2.

В этот раз не будем подробно расписывать каждое действие - укажем лишь ключевые шаги. Имеем:

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x ) = (2sin x + 5)’ = 2cos x ;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

Уравнение касательной:

y = 0 · (x − π /2) + 7 ⇒ y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет - просто мы наткнулись на точку экстремума.

Пусть дано уравнение f(x) = 0 . Число x называется корнем данного уравнения, если оно, будучи подставленным в уравнение, обращает его в равенство, то есть f(x) = 0 . Число x называют нулем функции f(x) .Нахождение корней уравнения с определенной точностью можно разделить на два этапа:

1) отделение корней, то есть установление промежутков, в которых содержится один корень уравнения;

2) вычисление корня, принадлежащего выбранному промежутку, с заданной точностью.

Известно, что если функция f(x) непрерывна и принимает на концах отрезка [a, b ] значения разных знаков, то есть f(a)× f(b) < 0 , то внутри этого отрезка найдется нуль функции.

Для отделения (или локализации) корня уравнения f(x) = 0 для непрерывной в области определения функции f(x) можно составить таблицу значений функции у = f(x) на определенном промежутке изменения аргумента х . Если для некоторых соседних значений аргумента значения функции имеют разные знаки, то нуль функции находится между ними.

Пусть дано уравнение f(x) = 0 , где функция f(x) непрерывна на отрезке [a, b ] и f(a)× f(b) < 0 .Для вычислениякорня данного уравнения
x Î [a, b ] находится середина этого отрезка x 1 = 0,5(a+b) . Если f(x 1) ¹ 0 , то для продолжения вычислений выбирается та из частей данного отрезка
[a, х 1 ] или [х 1 , b ] , на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначаются а 1 и b 1 . Новый отрезок [a 1 , b 1 ] снова делится пополам и производятся вычисления по изложенной схеме и так далее. В результате получается либо точный корень заданного уравнения на каком-то этапе, либо последовательность вложенных отрезков [a, b ] ,
[a 1 , b 1 ] , … , [a n , b n ] , …, таких что:

f(a n)× f(b n) < 0 , n =1, 2, …

Число x - общий предел последовательностей (а n) и (b n) – является корнем уравнения f(x) = 0 .

Оценка погрешности решения на n -ом шаге вычислений имеет вид.

Поэтому возникает естественное желание свести уравнение порядка выше первого к уравнению более низкого порядка. В некоторых случаях это удаётся сделать. Рассмотрим их.

1. Уравнения вида y (n) =f(x) решаются последовательным интегрированием n раз
, ,… .
Пример . Решить уравнение xy""=1 . Можем записать , следовательно, y"=ln|x| + C 1 и, интегрируя ещё раз, окончательно получаем y=∫ln|x| + C 1 x + C 2

2. В уравнениях вида F(x,y (k) ,y (k +1) ,..,y (n))=0 (то есть не содержащих в явном виде неизвестной функции и некоторых её производных) порядок понижается с помощью замены переменной y (k) = z(x). Тогда y (k +1) =z"(x),…,y (n) = z (n - k) (x) и мы получаем уравнение F(x,z,z",..,z (n - k)) порядка n-k. Его решением является функция z = φ(x,C 1 ,C 2 ,…,C n) или, вспоминая, что такое z, получаем уравнение y (n- k) = φ(x,C 1 ,C 2 ,…,C n - k) рассмотренного в случае 1 типа.
Пример 1 . Решить уравнение x 2 y"" = (y") 2 . Делаем замену y"=z(x) . Тогда y""=z"(x) . Подставляя в исходное уравнение, получаем x 2 z"=z 2 . Разделяя переменные, получаем . Интегрируя, имеем , или, что тоже самое, . Последнее соотношение записывается в виде , откуда . Интегрируя, окончательно получаем
Пример 2 . Решить уравнение x 3 y"" +x 2 y"=1 .Делаем замену переменных: y"=z; y""=z"
x 3 z"+x 2 z=1. Делаем замену переменных: z=u/x; z"=(u"x-u)/x 2
x 3 (u"x-u)/x 2 +x 2 u/x=1 или u"x 2 -xu+xu=1 или u"x^2=1. Откуда: u"=1/x 2 или du/dx=1/x 2 или u = int(dx/x 2) = -1/x+c 1
Поскольку z=u/x, то z = -1/x 2 +c 1 /x. Поскольку y"=z, то dy/dx=-1/x 2 +c 1 /x
y = int(c 1 dx/x-dx/x 2) =c 1 ln(x) + 1/x + c 2 . Ответ: y = c 1 ln(x) + 1/x + c 2

3. Следующим уравнением, допускающим понижение порядка, является уравнение вида F(y,y",y"",…,y (n))=0 , не содержащее в явном виде независимой переменной. Порядок уравнения понижается с помощью замены переменной y"=p(y) , где p - новая искомая функция, зависящая от y. Тогда
= и так далее. По индукции имеем y (n) =φ(p,p",..,p (n-1)). Подставляя в исходное уравнение, понижаем его порядок на единицу.

Пример . Решить уравнение (y") 2 +2yy""=0 . Делаем стандартную замену y"=p(y) , тогда y″=p′·p . Подставляя в уравнение, получаем Разделяя переменные, при p≠0, имеем Интегрируя, получаем или, что то же самое, . Тогда или . Интегрируя последнее равенство, окончательно получаем При разделении переменных мы могли потерять решение y=C, которое получается при p=0, или, что то же самое, при y"=0, но оно содержится в полученном выше.

4. Иногда удаётся подметить особенность, позволяющую понизить порядок уравнения отличными от рассмотренных выше способами. Покажем это на примерах.

Примеры .
1. Если обе части уравнения yy"""=y′y″ разделить на yy″, то получим уравнение , которое можно переписать в виде (lny″)′=(lny)′. Из последнего соотношения следует, что lny″=lny+lnC , или, что то же самое, y″=Cy . Получилось уравнение на порядок ниже и рассмотренного ранее типа.
2. Аналогично для уравнения yy″=y′(y′+1) имеем , или (ln(y"+1))" = (lny)" . Из последнего соотношения следует, что ln(y"+1) = lny + lnC 1 , или y"=C 1 y-1. Разделяя переменные и интегрируя, получаем, ln(C 1 y-1) = C 1 x+C 2
Решить уравнения, допускающие понижение порядка можно с помощью специального сервиса

Касательная - это прямая , которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой .

Выведем уравнение касательной, а затем - уравнение нормали к графику функции.

y = kx + b .

В нём k - угловой коэффициент.

Отсюда получаем следующую запись:

y - y 0 = k (x - x 0 ) .

Значение производной f "(x 0 ) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f (x 0 ) . В этом состоит геометрический смысл производной .

Таким образом, можем заменить k на f "(x 0 ) и получить следующее уравнение касательной к графику функции :

y - y 0 = f "(x 0 )(x - x 0 ) .

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль - это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали :

(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет "холодным душем".

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Найдём производную функции:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример - тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг - приведение уравнения к общему виду.

Пример 2.

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в "формулу-болванку" и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

.

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Находим уравнение касательной:

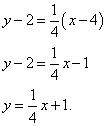
Перед тем, как привести уравнение к общему виду, нужно его немного "причесать": умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

.

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

.

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали - не заметить, что функция, данная в примере, - сложная и вычислять её производную как производную простой функции. Следующие примеры - уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция - сложная, так как аргумент тангенса (2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции.

Министерство образования и молодежной политики Чувашской Республики

БОУ ДПО (ПК) С «Чувашский республиканский институт образования»

Минобразования Чувашии

Кафедра математики и информационных технологий

Курсовая работа на тему:

« Функциональные уравнения. Методы их решения»

Выполнил (а): учитель математики МБОУ «СОШ № 60»

г. Чебоксары

Флегентова А.А.

Чебоксары, 2014

Введение……………………………………………………….……………..……3

Глава 1. Понятие функционального уравнения ………………………………...5

Глава 2. Практическая часть. Методы решения функционального уравнения.9

Заключение……………………………………………………………………….24

Список литературы………………………………………………………………25

Приложения……………………………………………………………………...26

Введение

Одно из важнейших математических умений, которым должны овладеть учащиеся школы, - умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, в уравнении могут участвовать целые, рациональные и другие числа, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение, решать, которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.

Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование. функциональный уравнение коши

Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе. Так как эта тема в школьном курсе не изучается в виду её сложности, при поступлении в престижные ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.

В настоящее время практически нет никаких пособий, обучающих решению функциональных уравнений.

Поэтому ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов решения функциональных уравнений.

Цель работы - выяснить, что является функциональным уравнением их системами, найти способы решения и составить сборник задач для использования математическими классами.

Задачи исследования:

1. изучение и анализ литературы;

2. поиск способов решения функциональных уравнений и их систем;

3. решение функциональных уравнений

4. составление сборника

Объект исследования: функциональные уравнения

Предмет исследования: изучение свойств и способов решения функциональных уравнений.

Структура: введение, понятие функционального уравнения, сборник задач, заключение.

Глава 1. Понятие функционального уравнения

Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют. Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях.

Некоторые функциональные уравнения знакомы нам еще из школьного курса это

f(x) = f(-x), f(-x) = - f(x), f(x+T) = f(x),

которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

этого уравнения, предполагая только непрерывность f(x).

Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

, (2)

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

.

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792-1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) - произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

Функциональному уравнению (3) удовлетворяют, в частности, функции:

Одними из простейших функциональных уравнений являются уравнения Коши

f(x+y) = f(x)+f(y), (4)

f(x+y) = f(x)·f(y), (5)

f(xy) = f(x)+f(y), (6)

f(xy) = f(x)·f(y), (7)

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид

, , ,

В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.

Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение - значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax . Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) - непрерывна, то это действительно так, если же данное предположение отбросить - то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.

Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) - класс функций, симметричных относительно прямой x = 1 , и т. д.

Глава 2. Практическая часть. Методы решения функционального уравнения

Простейшие функциональные уравнения

1. Пусть функция у =f(х) возрастает на R. Решите:

а) уравнение f(3х + 2) = f(4х 2 + х);

б) неравенство f(3х – 48) ≤ f(-х 2 + х).

Решение:

а) f(3х + 2) = f(4х 2 + х)

Есть такая теорема: если функция возрастает на промежутке Х, то каждое своё значение она принимает, а единственной точке. Поэтому,

3х+2 = 4х 2 + х;

4х 2 -2х-2=0;

2х 2 –x-1=0;

х 1 =1 и х 2 = -0,5

Ответ: х 1 =1 и х 2 = -0,5.

б) f(3х – 48) ≤ f(-х 2 + х);

3х-48 ≤ -х 2 + х;

х 2 + 2х – 48 ≤ 0;

х 1 =6 и х 2 = -8:

Ответ: [-8;6].

2. Пусть функция у =f(х) убывает на R. Решите неравенство f(2x-3)>f(х+2)

Решение:

Решаем также как и в предыдущем задании, только меняем знак у неравенства, так как функция убывает на R.

2х-3

Ответ: (-∞; 5).

Решение функциональных уравнений методом подстановки

Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.

1. Найдите все функции, определённые на множестве , удовлетворяющие соотношению

Решение

Придадим x значение . Получим

Отсюда

.

Получим систему

Из уравнения (1) выразим и подставим в уравнение (2).

; ;

Отсюда

; ; .

Проверим, действительно ли функция f(x) удовлетворяет уравнению

.

x=x - верно.

Ответ: .

Решение:

1) Пусть

2) Подставим в исходное уравнение, получим

3)Заменим z на получим или после преобразований в правой части уравнения:

4)Итак, получили два уравнения:

5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:

3. Пусть - некоторое действительное число. Найти функцию f(x) , определённую для всех x ≠ 1 и удовлетворяющую уравнению

,

где g – заданная функция, определённая при x ≠ 1 .

Решение: При замене

получаем систему

.

решением которой при a 2 ≠ 1 является функция

Ответ:

4. Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x) :

Решение: В первом уравнении сделаем подстановку 2x = 1/z .

При этом

и первое уравнение принимает вид:

Или

В результате получаем систему уравнений:

решение которой g(x) = 1/x, f(x) = x+1 .

Ответ: g(x) = 1/x, f(x) = x+1.

5. Найдите все функции f: R  R, которые при всех х, у € R удовлетворяют уравнению

f(х+у)=х+уf(х)+(1-х)у. (1)

Решение: Пусть f- функция удовлетворяющая (1). Поскольку (1) выполняется при всех значениях переменных х и у, то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у равное 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х. Таким образом, (1) => f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у € R.

6. Найдите все функции f: R  R, которые при всех х, у € R удовлетворяют уравнению

f(х+у)=х+уf(х)+(1-sin х)у (1)

Решение: точно также как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (1), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (1), то данное уравнение решений не имеет.

7. Найдите все функции f: R  R, которые при всех х, у € R удовлетворяют уравнению

f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1 (1)

Решение: поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1. Подставляя у= -1 в (1) получаем f(х)= х 2 -х+1 .

Ответ: f(х)= х 2 -х+1

8. Найдите все функции f: R  R, которые при всех х, у € R удовлетворяют уравнению

f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (1)

Решение: Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную (х или у). В данном случае, очевидно, проще получить у. Решив уравнение х 2 +6х+6)у=0 относительно х получаем х 1 = -1, х 2 = -5. Подстановка любого из этих значений в (1) дает нам f(у)=у 2 -4у.

Решение функциональных уравнений методом Коши

1. Найдите функцию , определённую на множестве натуральных чисел, удовлетворяющую условию

Где d - некоторое действительное число.

Решение:

Будем решать это уравнение по схеме, которая в математике называется методом Коши.

1. Найдём выражения для Получим

, .

2. Этот “эксперимент” подсказывает, что , где .

3. Проверим, действительно ли выполняется равенство

где . Применим для доказательства метод математической индукции.

1. Проверим, выполняется ли равенство при x=1: - верно.

2. Предположим, что равенство верно при , где , т.е.

Верно.

3. Докажем, что из этого следует равенство для x=n. Т.к. , то при x=n получим или

; .

Значит, равенство верно для любого натурального n . Таким образом, решением заданного функционального уравнения будет функция , где f(1)- произвольное число.

2. Найдите все непрерывные функции, удовлетворяющие условию

Решение:

Будем находить решение функционального уравнения постепенно, т.е. сначала найдём его решение, если является натуральным числом, затем – целым, потом рациональным и, наконец, - действительным.

1. Пусть y=x. Тогда .

2. При , получим

, , …

3. Докажем методом математической индукции, что при натуральных значениях (докажите это самостоятельно) . (1)

4. При x=1 получим . - постоянное число. Обозначим его через . Значит, для , имеем .

5. Положим в равенстве

(1) , где , получим

. Отсюда

или

.

Обозначив

через , получим

Значит, при положительном и рациональном x мы получим

Предполагая, что функция - непрерывна, получим

При

, .

6. Возьмём в равенстве . Получим

Отсюда .

Возьмём в этом равенстве

Получим

или

Т.к.

То

т.е. .

Итак, для любого действительного решением уравнения будет функция

Ответ:

Уравнение называется уравнением Коши.

3. Найдите непрерывные функции , удовлетворяющие условию

. (1)

Решение:

Попробуем свести это уравнение к функциональному уравнению Коши

с непрерывным решением

Пусть у=0 , тогда

.

Так как - постоянное число, обозначим его через и получим

.

Придадим теперь х значение .

Получим

.

Из уравнения (1)

получим

или

(2).

Решением уравнения (1) является функция

Значит, решением уравнения (2) будет функция

Ответ:

4. Найдите все непрерывные решения уравнений Коши:

a) f ( х y ) = f ( x ) + f ( y ) ( x, y € R \ { 0 } );

б ) f ( x + y ) = f ( xy ) ( x, y € R );

в ) f ( x + y ) = f ( x ) f ( y ) ( x, y €. R ) .

Решение:

Пусть вначале x > 0. Положим

g (x ) = f (e х ) .

Тогда

g (x + y ) = f (e х+у ) = f (e х e у ) = f (e х ) + f (e у ) = g (x ) + g (y ) , т. е. g (x )

удовлетворяет аддитивному уравнению Коши. Так как e х и f (x ) непрерывны, то и g (x ) непрерывна и имеет вид cx , где c- к онстанта. Тогда f (x ) имеет вид c ln x .

В частности,

f (1) = 0.

Положив

x = y = - 1,

получаем

f (1) = 2 f (- 1),

откуда

f (- 1) = 0.

Для произвольного x < 0 получаем

f (x ) = f (- x ) + f (- 1) = f (- x ).

Отсюда

f (x ) = c ln | x |

для произвольного

x ≠ 0.

б) Положив

y = 0,

получаем

f (x ) = f (0), т.е. f (x ) ≡ const.

Очевидно, что любая константа подходит.

в) Если

f (x ) = 0

для некоторого x ,

то

f (z ) = f (x ) f (z - x ) = 0

для любого z . В противном случае функция, будучи непрерывной, всюду имеет один и тот же знак. Так как

f (2 x ) = (f (x )) 2 ,

то этот знак положителен и можно рассмотреть непрерывную

функцию

g (x ) := ln f (x ). Имеем g (x + y ) = ln(f (x ) f (y )) = ln f (x )+ln f (y ) = g (x )+ g (y ),

т.е. выполнено аддитивное уравнение Коши. Отсюда g (x ) = cx для некоторого c , и

f (x ) = e сх .

Таким образом, либо

f (x )≡ 0, либо f (x ) ≡е сх .

Использование значений функции в некоторых точках

Иногда бывает невозможно найти подстановку, которая бы значительно упрощала бы вид уравнения. Однако, если зафиксировать одну из свободных переменных, некоторые члены уравнения могут также оказаться фиксированными. Для них можно ввести удобные обозначения и использовать при решении как обычные константы. Если эти константы войдут в ответ, проверка покажет, какие их значения являются допустимыми.

Решить уравнение

f(x+f(y))=xy

Решение: подстановка

у=0

даёт

f(x+f(0))=0.

На первый взгляд пользы мало, так как мы не знаем, чему равно f(0). Обозначим f(0)=с, тогда получаем f(х+с)=0. сделав замену переменной t=x+c (подстановка х=t-c), получаем f(е)=0, но такая функция, очевидно, не удовлетворяет исходному уравнению, поэтому решений нет.

Решить уравнение

f(x+f(y))=x+у

Решение: Снова сделаем подстановку у=0 и обозначим с=f(0), получим f(х+с)=х. Замена t=х+с дает f(t)=t-c. Несмотря, на то, что точное значение с нам известно, мы уже знаем, что лишь функция вида f(х)=х-с, где c=const, могут удовлетворять уравнению при всех х,у. чтобы найти с, подставим найденную функцию в исходное уравнение(заодно таким образом сделаем проверку):

f(x+f(y))=f(x+(y-c))=(x+(y-c))-c= x+y-2c.

Отсюда видим, что равенство

f(x+f(y))=x+у

для всех х,у при с равном 0 и только при нем. Поэтому ответ f(x)=x.

Ответ: f(x)=x.

Уравнение относительно

Найти все f: R  R такие, что (f(x))2 = 1

Решение: Рассматривая это как уравнение относительно неизвестного f(х), получаем

f ( x ) = 1 ;

f ( x ) = -1

Может показаться, что ответом будут две функции,

f(х)=1, f(х)=-1.

Однако, это не так. Рассмотрим, например функцию

1 х<0

1, х ≥ 0

Несложно видеть, что данная функция удовлетворяет уравнению. Какой же смысл придать совокупности? Поскольку исходное равенство должно выполнятся для всех х€ R, то есть для каждого х имеет место одно из равенств. Однако, неверным будет предположение, что одно из равенств выполняется сразу для всех х. Как мы увидели на примере, для одних х может выполнятся одно из равенств, а для других – другое. Попробуем охарактеризовать множество функций, задаваемое уравнением. Пусть А – множество тех х, для которых выполнено первое равенство. Тогда для всех остальных х должно быть выполнено второе. Мы видим, что множество А однозначно задает функцию f:

Ответ:

E ( f ) = {+-1} , где Е(f)

обозначает множество значений f.

Графическое решение функционального уравнения. При каких а и b для функции

f(х)=a|x-b| +3a|x-b |

выполнено условие при всех действительных

х: f(х)=f(f(х)) ?

Решение:

При а=0 функция f(х)=0, и уравнение, очевидно, удовлетворяется.

пусть а>0, тогда при больших х>0 функция

f(х)=а(х-b)+3a(x-b)=4ax-a(b+3b)>0

По рис.1 определяем, что возможно только равенство f(х)=х, если значения х достаточно велики и х>0. Конкретно, х>max{b;b }.

Следовательно, возможные значения для параметров a и b определяются из системы:

Которая имеет два решения:

При а=1/4, b=-1/3 получаем функцию

Ее график (рис.2) является графическим решением уравнения

f(х)=f(f(х))

Теперь предположим, что а<0, тогда при больших по абсолютной величине и х<0. Конкретно, х

Следовательно, возможные значения для параметров а и b определяются из системы

Которая имеет два решения

Если

a=-1/4, b=0,

то функция

f(х)=-|х|

удовлетворяет уравнению

f(х)=f(f(х))

Если a=-1/4, b=-1/3, тогда получаем функцию

А вот ее график (рис. 3) не является графическим решением уравнения f(х)=f(f(х)).

Ответ: , , ,

Заключение

В данной работе были рассмотрены функциональные уравнения и некоторые способы их решения. В ходе работы мы убедились, что функциональные уравнения – это общий класс уравнений, в которых искомой является некоторая функция. К функциональным уравнениям по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях. Под функциональным уравнением в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональное уравнение можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.

Список литературы

Размещено на Allbest.ru

ПРИЛОЖЕНИЯ

Рис.1

Рис.2

Рис.3

Размещено на Allbest.ru